|
Conjunto no vacío y finito de elementos, distintos
entre sí e identificados, por ejemplo: números,
letras, combinaciones entre ellos.
Simbología:
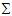
Ejemplo: sea
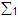 = =
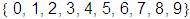 y y
“2 es un símbolo del alfabeto” se denota: 2
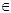 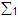 . .
Otros ejemplos: 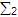 = =
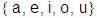
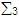 = =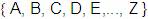 ,
el alfabeto de letras mayúsculas. ,
el alfabeto de letras mayúsculas.
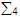 = =
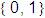 ,
el alfabeto binario ,
el alfabeto binario
Operaciones
con Alfabetos
Los Alfabetos, en su condición de conjuntos, pueden
ser sometidos a las operaciones clásicas de la
Teoría
de Conjuntos, es decir Unión,
Intersección, Diferencia y Complementación de
Conjuntos.
Las propiedades más importantes de dichas
operaciones son:
Si
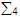 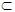 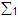  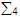  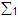 = = 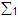
Si
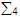 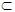 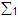  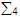 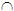 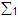 = = 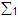
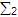  ( (
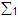  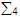 )
= ( )
= (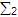
 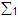 ) )
 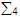
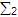 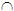 ( (
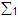 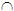 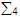 )
= ( )
= (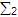
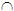 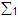 ) )
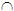 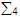
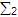 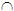 ( (
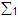  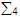 )
= ( )
= (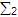
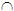 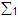 ) )
 ( (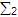
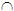 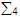 ) )
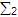  ( (
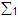 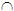 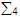 )
= ( )
= (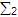
 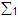 ) )
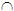 ( (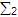
 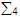 ) )
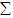  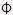 = =
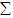 y y
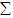 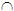 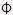 = =
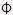
Potencia de un alfabeto
Si 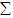 es
un alfabeto, es posible expresar el conjunto de
todas las cadenas de cierta longitud de dicho
alfabeto utilizando una notación exponencial.
Definimos como es
un alfabeto, es posible expresar el conjunto de
todas las cadenas de cierta longitud de dicho
alfabeto utilizando una notación exponencial.
Definimos como 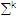 . .
Como el conjunto de cadenas de longitud k, tales que
todos los símbolos que las forman pertenecen a 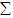 . .
Ejemplo:
Si 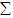 = = 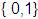 ,
entonces ,
entonces 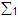 = = 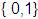 ; ; 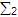 = =  ; ;
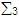 = = 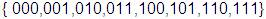
Nótese además que independiente, de cual sea el
alfabeto siempre 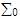 = = 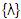 ,
siendo ,
siendo 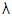 la
única cadena cuya longitud es 0. la
única cadena cuya longitud es 0.
Otra cuestión que se presta a confusión es la
diferencia que existe entre 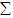 = = 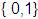 ,
y ,
y 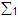 = = 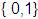 ,
donde la primera es un alfabeto con símbolos cero y
uno y el segundo es un conjunto de cadenas de
longitud unitaria. ,
donde la primera es un alfabeto con símbolos cero y
uno y el segundo es un conjunto de cadenas de
longitud unitaria.
PALABRA
Se llama Palabra, Cadena o Tira a la concatenación o
secuencia finita de elementos de un alfabeto.
Simbología:
Las palabras se denotan con las últimas letras del
alfabeto en minúscula (x = “001” , y = “ai”)
Ejemplo:

Longitud de una
palabra.
Cada palabra tiene su longitud, es decir, el número
o la cantidad de elementos que la componen.
Simbología:
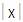 (se
utilizan dos barras a los costados de la palabra) (se
utilizan dos barras a los costados de la palabra)
Ejemplo: sean las palabras: x = “001”, y =
“ai”, z = “ZXABK”
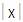 = 3
= 3
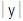 = 2
= 2
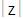 = 5
= 5
La
longitud de una palabra o cadena puede asumir
distintos valores, si la longitud es igual a 1, la
palabra es igual al elemento o símbolo del alfabeto,
es decir, que cada elemento o símbolo de un alfabeto
puede ser una tira o cadena del mismo.
Ejemplo: “0”
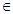 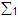
“A”
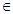 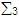
Palabra Vacía.
Si la longitud de una palabra es igual a 0, estamos
frente a una palabra que existe pero que no contiene
elementos, llamada “palabra vacía” y es una cadena
sobre cualquier alfabeto.
Simbología:
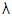
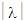 =
0 =
0
Subpalabras: Prefijo y Sufijo.
Se denota Sufijo a la subcadena
de una palabra dada formada por los primeros
símbolos de la misma y Prefijo a la subcadena
formada por los últimos símbolos de dicha palabra,
es decir, sea v una cadena sobre una
alfabeto, se llama Sufijo a la subcadena x
y Prefijo a la subcadena y de v,
tal que v = xy
Ejemplo: v = “aeiou”
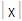 = 3
= 3
 x
= “aei” x
= “aei”
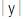 =
2 =
2
 x
= “ou” x
= “ou”
Universo de discurso
Se llama Universo de Discurso o Lenguaje
Universal al conjunto de todas las cadenas,
tiras o palabras que se pueden formar con los
elementos o símbolos de un alfabeto, incluida la
palabra vacía.
Simbología:
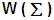
El
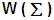 es
una conjunto infinito ya que son infinitas las
palabras o cadenas que puedo formar con los símbolos
de un alfabeto ya que éstos no son vacíos. es
una conjunto infinito ya que son infinitas las
palabras o cadenas que puedo formar con los símbolos
de un alfabeto ya que éstos no son vacíos.
Ejemplo:
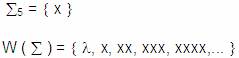
Operaciones palabras
Concatenación
La
Concatenación de dos palabras (s, t) da origen a una
nueva palabra (r) formada por los elementos o
símbolos de la primera palabra seguidos los símbolos
de la segunda, es decir, r = s
 t t
Ejemplo: siendo las palabras:
s = “abc” t = “defg”
r = s
 t
= “abcdefg” t
= “abcdefg”
Simbología:
la concatenación se indica con un punto entre las
palabras a concatenar.
La concatenación se puede realizar entre
la palabra vacía y cualquier palabra, teniendo como
resultado la misma palabra sin ser modificada.
Ejemplo:
s
 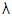 = =
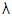  s
= s s
= s
Propiedades de la operación Concatenación:
Propiedad Conmutativa: ésta propiedad no se cumple
para esta operación: s
 t
¹ t t
¹ t
 s s
Operación Cerrada: la concatenación de dos palabras
que pertenecen a
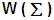 es
también una palabra de es
también una palabra de
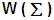 . .
Propiedad Asociativa: (r
 s) s)
 t
= r t
= r
 (s (s
 t) t)
Potenciación
Se llama Potencia de una palabra v a la nueva
palabra z que se obtiene de haber concatenado
v consigo misma tantas veces como indica el
exponente:
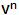 = v. v. v. v. v. v. ... n
= v. v. v. v. v. v. ... n
Ejemplo:
sea v = “011”
Z =
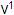 =
v = “011” =
v = “011”
Z =
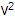 =
v =
v
 v
= “011011” v
= “011011”
Z =
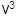 =
v =
v
 v v
 v
= “011011011” v
= “011011011”
Toda potencia 0 de una palabra, por definición, es
la palabra vacía:
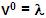
Reflexión
La Reflexión o refleja de una palabra o cadena x,
se forma invirtiendo el orden de los símbolos o
elementos de la misma.
Ejemplo:
x = “abc”
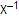 =
“cba” =
“cba”
|

