|
CONSTRUCCIÓN DE AUTÓMATA FINITO
Ejercicio 1:
Diseñar un autómata finito que acepte una cadena
formada por 4 bits, debiendo ser el primer elemento
igual al tercero.
Ejercicio 2:
Diseñar un autómata finito que acepte aquellas
cadenas de longitud 3 (tres), que tengan dos
símbolos iguales seguidos, cuyo alfabeto está
formado por dos símbolos distintos (S = {a, b}).
MINIMIZACIÓN DE AUTÓMATA FINITO
Minimizar y determinar si los siguientes AFD son
equivalentes: a) eliminar estados no conexos, b)
minimizar cada autómata (demostración paso por
paso), c) tabla y grafo del AFD minimizado, d)
definición formal del autómata.
f1
|
a |
b |
|
®A |
C |
A |
|
B |
B |
A |
|
*C |
C |
B |
a) todos los estados son conexos.
b) minimización:
Q/E0 = ( C0 = {C}, C1 = {A, B})
f(A,
a) = C e C0 f(B, a) = B e C1
f(A,
b) = A e C1 f(B, b) = A e C0
“LOS ESTADOS A Y B, NO SON EQUIVALENTES, POR LO
TANTO NO SE MINIMIZA”
c)
y d) iguales al AFD inicial.
f2
|
a |
b |
|
®A |
B |
D |
|
B |
B |
C |
|
C |
D |
B |
|
*D |
D |
B |
AUTOMATA F2:
a) todos los estados son conexos
b) minimización:
Q/E0 = ( C0 = {D}, C1 = {A, B,C})
f(A,
a) = B e C1 f(B, a) = B e
C1 f(C, a) = D e C0
f(A,
b) = D e C0 f(B, b) = C e
C1 f(C, b) = B e C1
“LOS ESTADOS A, B Y C , NO SON EQUIVALENTES, POR LO
TANTO NO SE MINIMIZA”
Q/E1 = ( C0 = {D}, C1 = {A}, C2 = {B}, C3 = {C} )
c)
y d) iguales al AFD inicial.
"LOS AUTOMATAS F1 Y F2 NO SON EQUIVALENTES”
AUTÓMATA FINITO NO DETERMINISTA: ELIMINACIÓN DE
Ejercicio
1:
|
|
1 |
2 |
|
|
®a |
a,b |
d |
b |
|
b |
c,d |
a |
c,d |
|
c |
d |
c,d |
|
|
*d |
b |
b,c |
c |
a) Determinar si las siguientes cadenas son
aceptadas:
X1 = “122” x2 = “122” X3 =
“212”
b)
eliminar
 .
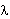Ejercicio 2: Obtener el AFD equivalente
|
|
a |
b |
c |
|
|
®p |
|
|
|
q,t |
|
q |
|
r,s |
|
r,s |
|
r |
|
|
|
q,u |
|
s |
t,p |
|
u |
|
|
t |
|
v |
|
q |
|
u |
s,q |
|
v |
s |
|
*v |
|
|
|
r |
a) Determinar si las siguientes cadenas son
aceptadas:
X1 = “bbcc” x2 = “acbcac” X3 = “bcacaa”
X4 = “caa” x5 = “abac”
b)
eliminar
.
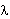Solución:
T = { (p,p), (p,q), (p,t), (q,q), (q,r), (q,s),
(r,r), (r,q), (r,u), (t,t), (t,q), (u,u), (u,s),
(v,v), (v,r),(s,s)}
T*
= { (p,p), (p,q), (p,t), (p,r), (p,s), (p,u)
(q,q), (q,r), (q,s), (q,u)
(r,r), (r,q), (r,u), (r,s)
(s,s)
(t,t), (t,q), (t,r), (t,s), (t,u)
(u,u),
(u,s)
(v,v), (v,r), (v,u), (v,s), (v,q)}
CONSTRUCCIÓN DE AUTÓMAS FINITOS
Dada las siguientes reglas de producción:
P1 = {S ::= l, S::= xX, S::= y Y, Y::= yY, Y::= x,
X::= xX, X::=y}
P2 =
{A
::= 0A, A::=1B, B::= 0C, B::= 0D, C::= 0, C:::= 1B,
C::= 1D, D::= 1, D::= 1A}
Se
pide:
a) la definición de todos los componentes de la
gramática formal
b) construir A.F. correspondiente
c) la definición de cada uno de los componentes
que define el A.F.
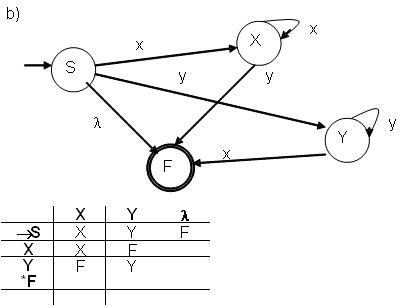
P1
a) G1 = ( {x,y}, {S, X,Y}, S,
P1) c) E
= {x, y} Q = {S, X, Y, F}
q0 = {S}
F = F
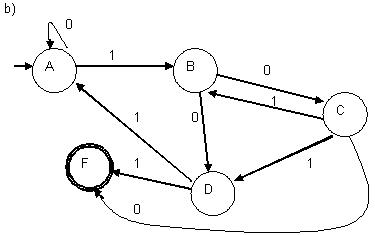
P2:
a) G2 = ( {0,1}, {A, B, C, D, F}, A, P2)
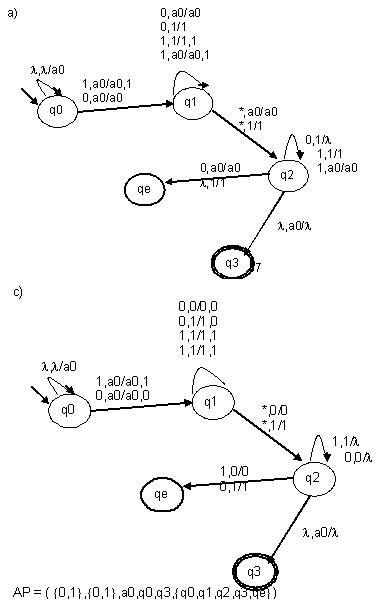
AUTÓMATA A PILA
Diseñar un A.P. (por cada items) que verifique si
dos nibles leídos, separados por un * (asterisco):
a) El primero tienen la misma cantidad de 1
que 0 el segundo.
b) El primer nible constituye la imagen refleja
del segundo.
SOLUCIÓN
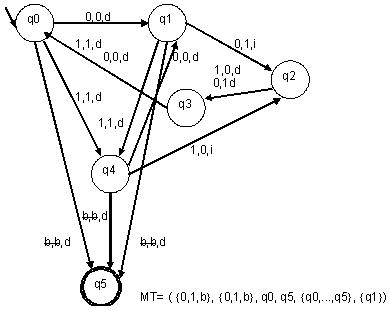
MÁQUINA DE TURING
Ejercicio
1:
Diseñar una M. De T. que dada una palabra, encuentra
las subtiras “00” y las cambie por “11” y las
subtiras “11” las cambie por “00”. La palabra
finaliza cuando se lee un b (blanco). El
cabezal se encuentra sobre el 1er. bit de la tira.
¯
Ejemplo: b 010010110011
b
Salida: b 011110001100
b
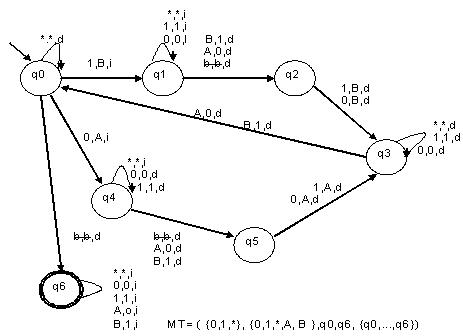
Ejercicio 2:
Diseñar un M. De T. que copie el segundo nible
sobre el primero, se encuentran separados por un *
(asterisco). El cabezal se encuentra sobre el *
(asterisco). Ej.:
¯
Entrada: b1001*0011b
Salida: b0011*0011b
|
EJERCICIOS RESUELTOS:
AUTÓMATA FINITO, AUTÓMATA A PILA Y MAQUINA DE TURING